Terminology: Review

Feb 18, 2024
All notes are expanded based on

A function is in Direct Style when it returns its result back to the caller.

A function is in Continuation Passing Style when it, and every function call in it, passes its result to another function.

A Tail Call occurs when a funciton returns the result of another fucntion call without any more computations (e.g. tail recursion)

Instead of returning the result to the caller, we pass it forward to another function giving the computation after the call.

Instead of returning the result to the caller, we pass it forward to another function giving the computation after the call.

CPS Transformation

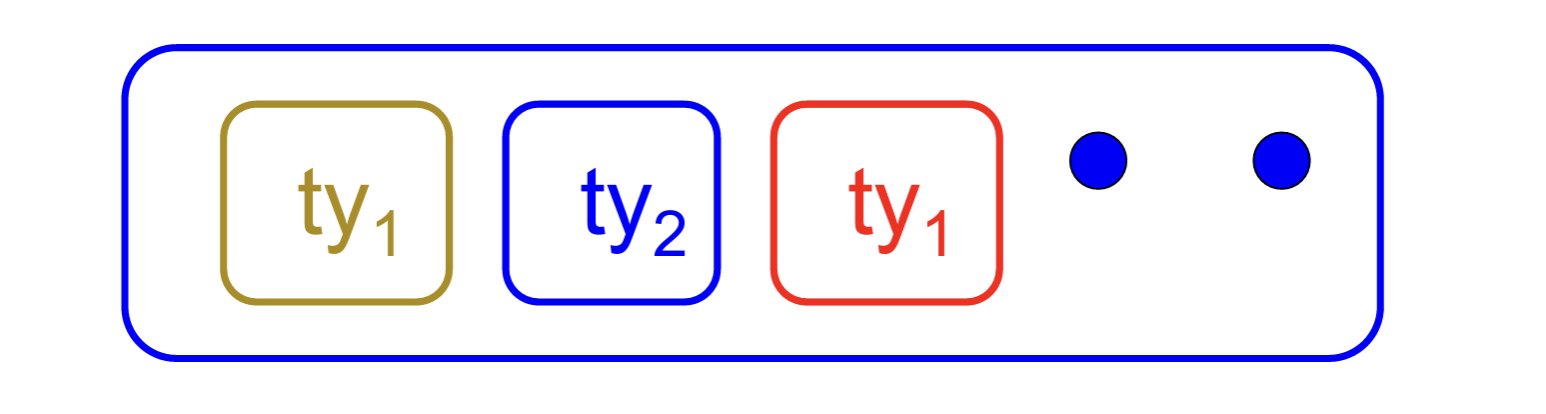
Step 1: Add continuation argument to any function definition:

Let f arg = e $\Rightarrow$ let f arg k = e
Idea: Every function takes an extra parameter saying where the result goes

Step 2: A simple expression in tail position should be passed to a continuation instead of returned:

return a $\Rightarrow$ k a
Assuming a is a constant or variable.
“Simple” = “No available function calls.”

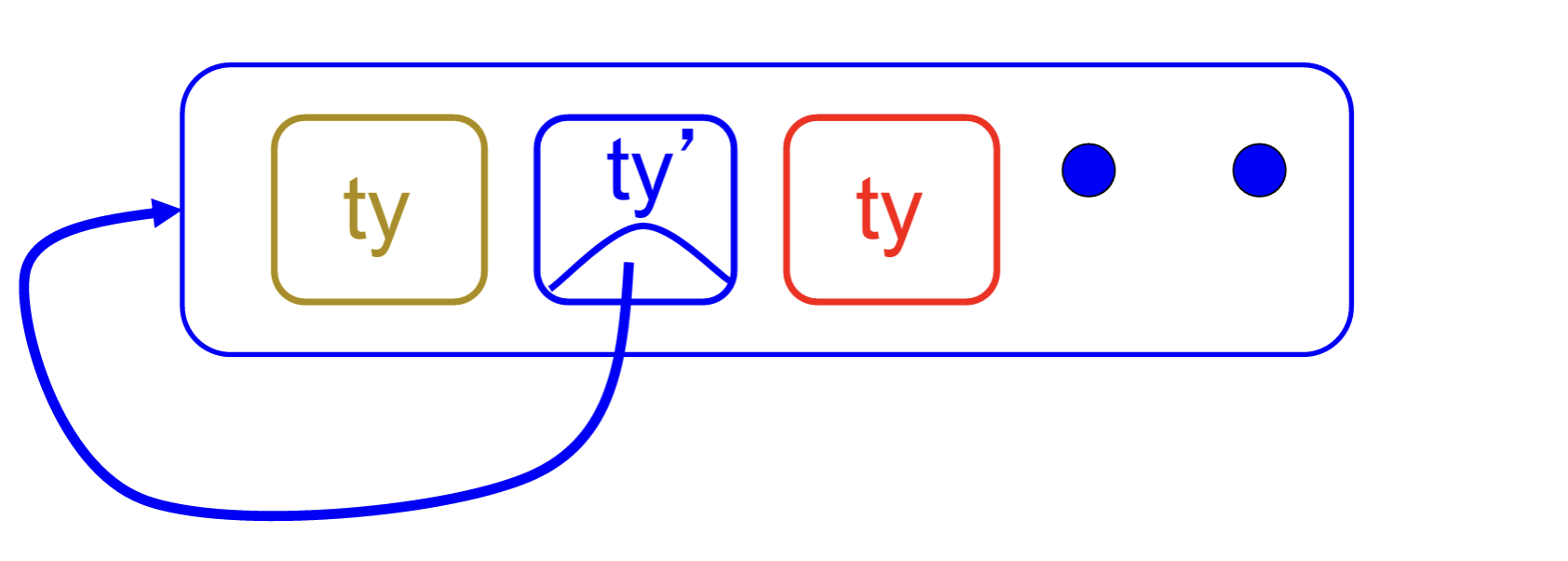
Step 3: Pass the current continuation to every function call in tail position.

return f arg $\Rightarrow$ f arg k
The function “isn’t going to return,” so we need to tell it where to put the result.

Step 4: Each function call not in tail position needs to be converted to take a new continuation (containing the old continuation as appropriate)

return op (f arg) $\Rightarrow$ f arg (fun r -> k(op r))
op represents a primitive operation
return g(f arg) $\Rightarrow$ f arg (fun r -> g r k)

Example

Before:	After:
`let rec add_list lst = match lst with [] -> 0 \| (0::xs) -> add_list xs \| (x::xs) -> (+) x (add_list xs)`	`let rec add_listk k = match lst with (* rule 1 ) \| [] -> k 0 ( rule 2 ) \| (0::xs) -> add_list xs k ( rule 3 ) \| (x::xs) -> add_list xs (fun r -> k ((+) x r)) ( rule 4 *)`

Before:

After:

let rec add_list lst = 
    match lst with [] -> 0
    | (0::xs) -> add_list xs 
    | (x::xs) -> (+) x (add_list xs)

let rec add_listk k = 
    match lst with      (* rule 1 *)
    | [] -> k 0         (* rule 2 *) 
    | (0::xs) -> add_list xs k  (* rule 3 *)
    | (x::xs) -> add_list xs 
                (fun r -> k ((+) x r))
                    (* rule 4 *)

Example 2

Before:	After:
`let rec mem (y, lst) = match lst with [] -> false \| (x::xs) -> if x = y then true else mem(y, xs)`	`let rec memk (y, lst) k = match lst with (* rule 1 ) \| [] -> k false \| (x::xs) -> ( rule 2 ) eqk (x, y) (fun b -> if b then ( rule 4 ) k true ( rule 2 ) else memk (y, xs) k ( rule 3 *))`

Before:

After:

let rec mem (y, lst) = 
    match lst with [] -> false 
    | (x::xs) -> 
        if x = y then 
            true 
        else 
            mem(y, xs)

let rec memk (y, lst) k =
    match lst with      (* rule 1 *)
    | [] -> k false  
    | (x::xs) ->        (* rule 2 *)
        eqk (x, y)
        (fun b -> 
            if b then  (* rule 4 *)
                k true (* rule 2 *)
            else memk (y, xs) k 
            (* rule 3 *))

Data type in Ocaml: lists

Frequently used lists in recursive program

Matched over two structural cases

$[]$ - the empry list
$(x :: xs)$ a non-empty list

Covers all possibel lists
$type ‘a list = [] | (::) of ‘a * ‘a list$

Not quite legitimate declaration because of special syntax

Variants - Syntax (slightly simplified)

$type name = C_{1} [of t y_{1}] | \dots | C_{n} [of t y_{n}]$

Introduce a type called name
$(fun - > C_{i} x) : t y_{1} - > name$
$C_{i}$ is called a constructor; if the optional type argument is omitted, it is called a constant
Constructors are the basis of almost all pattern mathcing

Enumeartion Types as Variants

An enumeration type is a collection of distinct values

In C and Ocaml they have an order structure; order by order of input

type weekday = Monday | Tuesday | Wednesday | Thursday | Friday 
    | Saturday | Sunday

Functions over Enumerations

let day_after day = match day with 
    Monday -> Tuesday 
    | Tuesday -> Wednesday
    | Wednesday -> Thursday
    | Thursday -> Friday 
    | Friday -> Saturday
    | Saturday -> Sunday
    | Sunday -> Monday


let rec days_later n day =
    match n with 0 -> day
    | _ -> if n > 0 
            then day_after (days_later (n -1) day)
            else days_later (n + 7) day

# days_later 2 Tuesday;;
- : weekday = Thursday
# days_later (-1) Wednesday;;
- : weekday = Tuesday
# days_later (-4) Monday;;
- : weekday = Thursday

Problem:

Write a function $is_weekend : weekday bool$

let is_weekend day =
    match day with 
    Saturday -> true
    | Sunday -> true
    | _ -> false

Example Enumeration Types

type bin_op = IntPlusOp | IntMinusOp
        | EqOp | CommaOp | ConsOp

type mon_op = HdOp | TlOp | FstOp
        | SndOp

Explanantion of $bin_op type$

We create a type name bin_op (short for binary operator), which can take one of the following five values:

$IntPlusOp$ represents an operation for integer addition.

$IntMinusOp$ represents an operation for integer subtraction.

$EqOp$ represents an equality operation.

$CommaOp$ represents a comma operator.

$ConsOp$ represents the cons operation, to construct lists or combine an element with a list.

Explanantion of $mon_op type$

We create a type name mon_op (short for monadic or unary operator), which can take one of the following five values:

$HdOp$ represents head of list (the first element)

$TlOp$ represents the tail of the list (the last element)

$FstOp$ represents an operation to get the first element of a tuple

$SndOp$ represents an operation to get the second element of a tuple.

$ConsOp$ represents the cons operation, to construct lists or combine an element with a list.

Disjoint Union Types

Disjoint union types, with some possibly occurring more than once

We can also add in some new singleton elements

type id = DriversLicense of int 
    | SocialSecurity of int | Name of string

let check_id id = match id with 
    DriversLicense num -> 
        not (List.mem num[13570; 99999])
        | SocialSecurity num -> num < 900000000
        | Name str -> not (str = "John Doe")

Problem:

Create a type to represent the currencies for US, UK, Europe and Japan

type currency = 
    Dollar of int 
    | Pound of int 
    | Euro of int
    | Yen of int

Example Disjoint Union Type

type const = 
    BoolConst of bool
    | IntConst of int 
    | FloatConst of float 
    | StringConst of float
    | NilConst 
    | UnitConst

type const = BoolConst of bool
    | IntConst of int | FloatConst of float 
    | StringConst of string | NilConst
    | UnitConst

How do we represnet 7 as a const?

Answer: $IntConst 7$

Polymorphism in Variants

The type $‘a option$ gives us something to represent non-existence or failure

type `a option = Some of `a | None

Used to encode partial functions

Often can replace the raising of an exception

Functions producing option

# let rec first p list = 
    match list with [] -> None 
    | (x::xs) -> if p x then Some x else first p xs
val first : (`a -> bool) -> `a lost -> a` option = <fun>

# first (fun x -> x > 3) [1;3;4;2;5];;
- : int option = Some 4
# first (fun x -> x > 5) [1;3;4;2;5];;
- : int option = None

Functions over option

# let result_ok r = 
    match r with None -> false
    | Some _ -> true;;
val result_ok : `a option -> bool = <fun>
# result_ok (first (fun x -> x > 3) [1;3;4;2;5]);;
- : bool = true
# result_ok (first (fun x -> x > 5) [1;3;4;2;5]);;
- : bool = false

Problem:

Write a hd and tl on lists that doesn’t raise an exception and works at all types of lists.

let hd list = 
    match list with [] -> None
    | (x::xs) -> Some x

let tl list = 
    match list with [] -> none
    | (x::xs) -> Some xs

Mapping over Variants

# let optionMap f opt = 
    match opt with None -> None
    | Some x -> Some (f x)
val optionMap : (`a -> `b) -> `a option -> `b
    option = <fun>
# optionMap (fun x -> x - 2)
    (first (fun x -> x > 3) [1;3;4;2;5]);;
- : int option = Some 2

Folding over Variants

# let optionFold someFun noneVal opt = 
    match opt with None -> noneVal
    | Some x -> someFun x;;
val optionFold : (`a -> `b) -> `b -> `a option -> 
    `b = <fun>
# let optionMap f opt = 
    optionFold (fun x -> Some(f x)) None opt;;
val optionMap : (`b -> `b) -> `a option -> `b 
    option = <fun>

Recursive Types

The type being defined may be a component of itself

Recursive Data Types

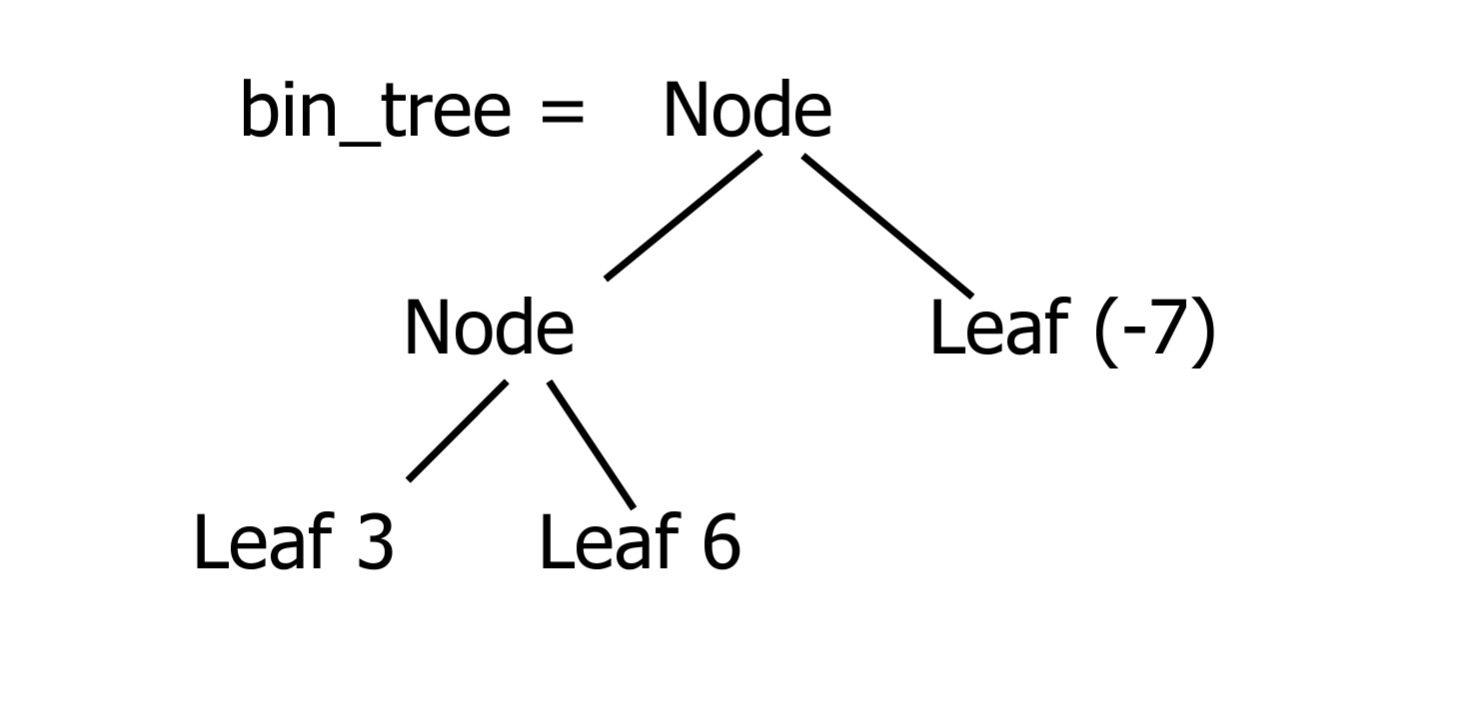
type int_Bin_Tree = 
    Leaf of int | Node of (int_Bin_Tree * int_Bin_Tree)

Recursive Data Types Values

let bin_tree = 
    Node(Node(Leaf 3, Leaf 6), Leaf(-7))

Recursive Functions

let rec first_leaf_value tree = 
    match tree with (Leaf n) -> n
    | Node (left_tree, right_tree) -> 
    first_leaf_value left_tree

# let left = first_leaf_value bin_tree
val left : int = 3

Recursive Data Types

type exp = 
    VarExp of string
    | ConstExp of const
    | MonOpAppExp of mon_op * exp
    | BinOpAppExp of bin_op * exo * exp 
    | IfExp of exp * exp * exp 
    | AppExp of exp * exp 
    | FunExp of string * exp

# type bin_op = IntPlusOp | IntMinusOp | EqOp | CommaOp 
    | ConsOp | ...

# type const = BoolConst of bool | IntConst of int |
...

# type exp = VarExp of string | ConstExp of const | 
    BinOpAppExp of bin_op * exp * exp | ...

How to represent 6 as an exp?

Answer: ConstExp (IntConst 6)

How to represent (6, 3) as an exp?

BinOpAppExp (CommaOp, ConstExp (IntConst 6), ConstExp(IntConst 3))

How to represent [(6, 3)] as an exp?

BinOpAppExp(ConstOp, BinOpAppExp(CommaOp, ConstExp(IntConst 6), ConstExp(IntConst 3)), ConstExp NilConst)

Problem

type int_Bin_Tree = Leaf of int 
    | Node of (int_Bin_Tree * int_Bin_Tree)

Write sum_tree : int_Bin_Tree -> int
Adds all ints in tree
let rec sum_tree t =

let rec sum_tree t = 
    match t with Leaf n -> n
    | Node(t1, t2) -> sum_tree t1 + sum_tree t2

How to count the number of variables in an exp?

let rec varCnt exp = 
    match exp with VarExp x -> 1
    | ConstExp c -> 0 
    | BinOpAppExp (b, e1, e2) ->  varCnt e1 + varCnt e2
    | FunExp (x, e) -> 1 + varCnt e
    | AppExp (e1, e2) ->  varCnt e1 + varCnt e2

Mapping over Recursive Types

let rec ibtreeMap f tree = 
    match tree with (Leaf n) -> Leaf (f n)
    | Node (left_tree, right_tree) -> 
    Node (ibtreeMap f left_tree, ibtreeMap f right_tree)

# ibtreeMap ((+) 2) bin_tree;;
- : int_Bin_Tree = Node (Node (Leaf 5, Leaf 8), Leaf(-5))

Folding over Recursive Types

# let rec ibtreeFoldRight leafFun nodeFun tree = 
    match tree with Leaf n -> leafFun n
    | Node (left_tree, right_tree) -> 
    nodeFun 
    (ibtreeFoldRight leafFun nodeFun left_tree)
    (ibtreeFoldRight leafFun nodeFun right_tree);;
val ibtreeFoldRight : (int -> `a) -> (`a -> `a -> `a) -> 
    int_Bin_Tree -> `a = <fun>

# let tree_sum = 
    ibtreeFoldRight (fun x -> x) (+);;
val tree_sum : int_Bin_Tree -> int = <fun>
# tree_sum bin_tree;;
- : int = 2

Mutually Recursive Types

type `a tree = TreeLeaf of `a 
    | TreeNode of `a treeList 
and a` treeList = Last of `a tree
    | More of (`a tree * `a treeList);;
type `a tree = TreeLeaf of `a | TreeNode of `a
    treeList
and `a treeList = Last of `a tree | More of (`a 
    tree * `a treeList)

Mutually Recursive Types - Values

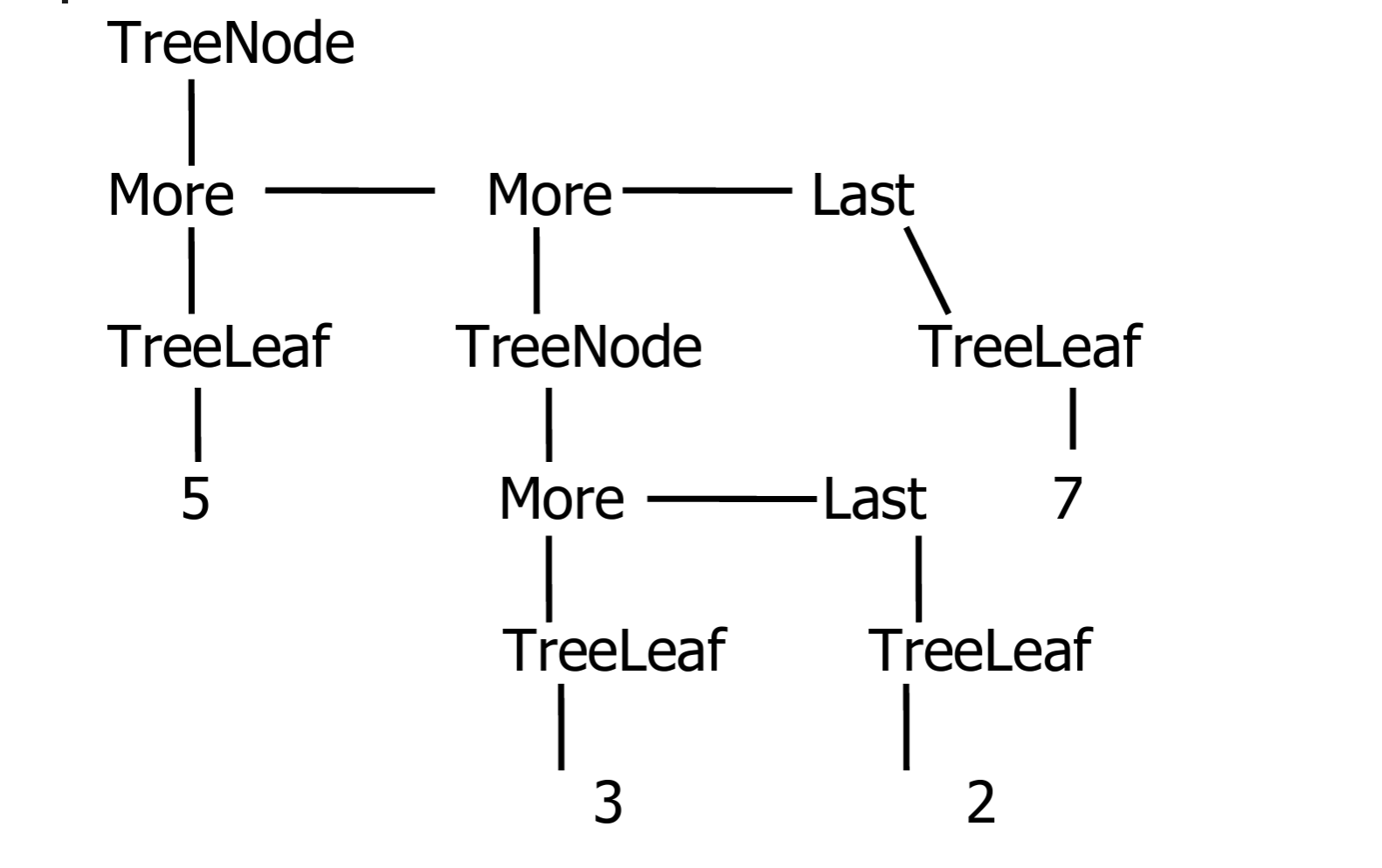
let tree = 
    TreeNode
    (More (TreeLeaf 5, 
        More(TreeNode 
            More(TreeLeaf 3, 
                Last(TreeLeaf 2))),
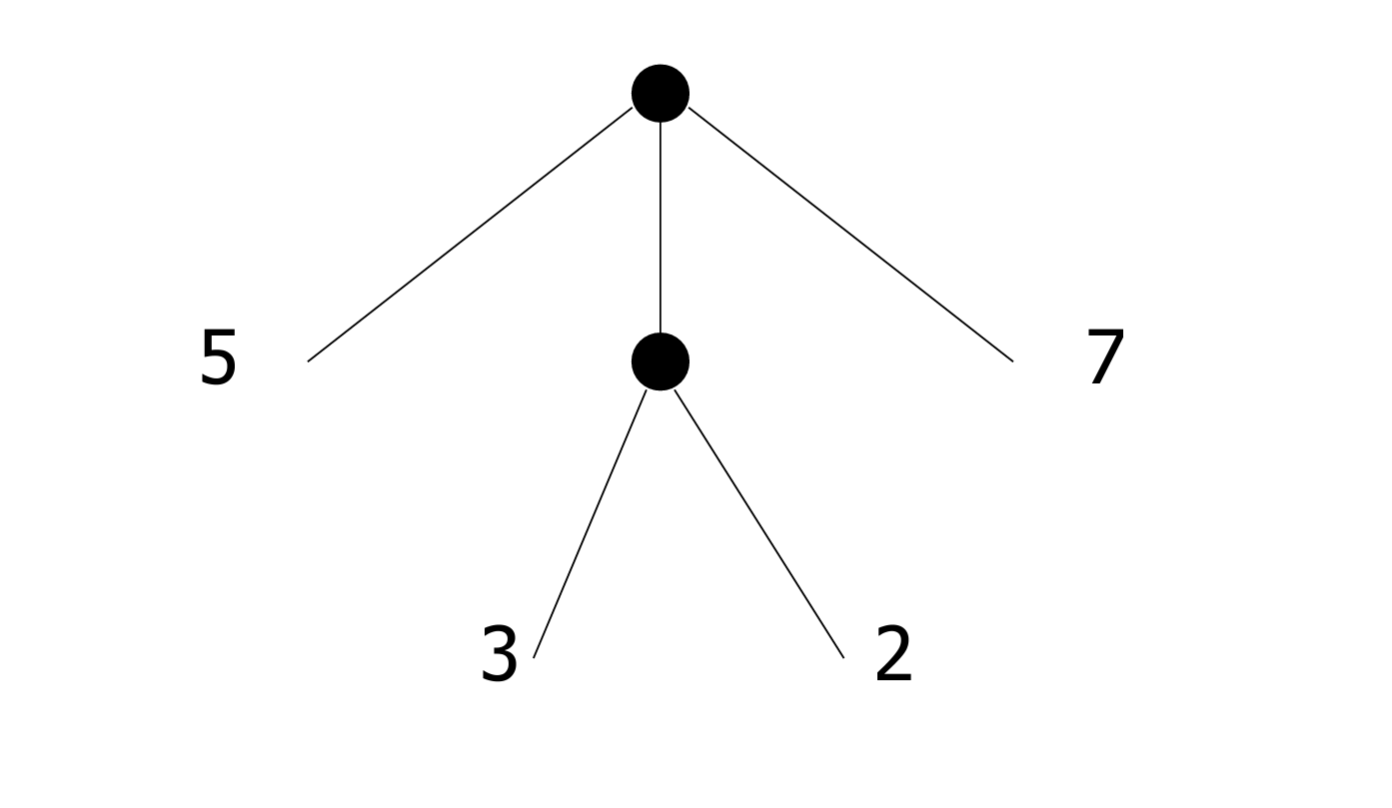
            Last (TreeLeaf 7)))

A more conventional picture

Mutually Recursive Functions

# let rec fringe tree = 
    match tree with (TreeLeaf x) -> [x]
    |(TreeNode list) -> list_fringe list
and list_fringe tree_list = 
    match tree_list with (Last tree) -> fringe tree 
    | (More (tree, list)) -> 
        (fringe tree) @ (list_fringe list);;

val fringe : `a tree -> `a list = <fun> 
val list_fringe : `a treeList -> `a list = <fun> 

# fringe tree;;
- : int list = [5; 3; 2; 7]

Problem

# type `a tree = TreeLeaf of `a | TreeNode of `a a treeList 
and `a treeList = Last of `a tree | More of (`a tree * `a treeList);;

$Define tree_size$

let rec tree_size t = 
    match t with TreeLeaf _ -> 1
    | TreeNode ts -> treeList_size ts
and treeList_size ts = 
    match ts with Last t -> 
    | More t ts` -> tree_size t + treeList_size ts`

Nested Recursive Types

type `a labeled_tree =    
    TreeNode of (`a * `a labeled_tree list)

let ltree = 
    TreeNode(5, 
    [TreeNode (3, []);
    TreeNode (2, [TreeNode (1, []);
            TreeNode (7, [])]);
    TreeNode (5, [])])